For the final output layer, especially in classification tasks (like predicting the next token in a LLM), we want probabilities. We want to know: “What is the % chance that this token is Next?”
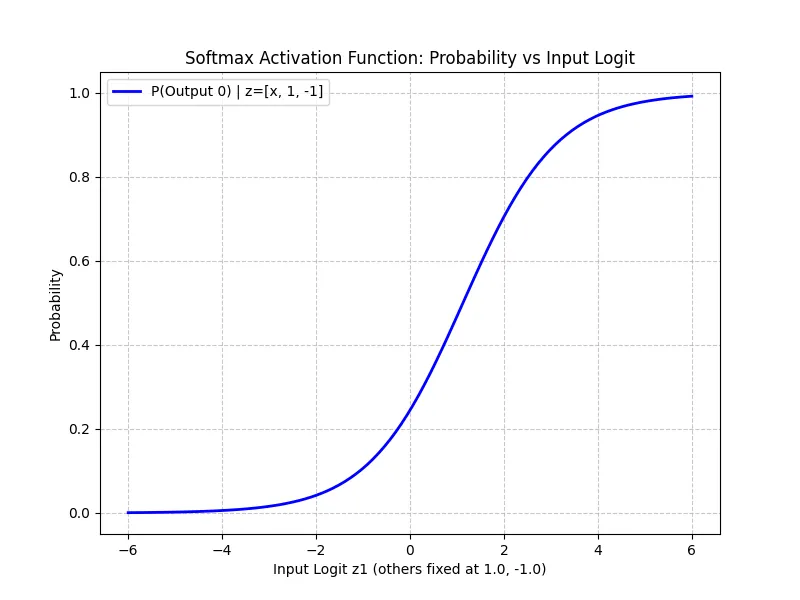
Softmax function takes raw numbers (logits) and converts them into a probability distribution summing to 1.
“Sigma of z, sub i, equals e to the power of z, sub i, divided by the sum from j equals 1 to K, of e to the power of z, sub j.”
Softmax Normalization is a mathematical function often used in machine learning (and the Attention Mechanism) to convert a vector of raw scores (logits) into a probability distribution.
Why Use Softmax for Attention?
- Interpretability: It ensures all values sum to 1.0, allowing us to interpret them as probabilities or attention percentages.
- Handling Extreme Values: Compared to simple normalization (summation), Softmax handles extreme values better.
- If one score is significantly higher (e.g., 400 vs 1, 2, 3), simple normalization might still give non-zero weight to small values (e.g., 0.0025) and not quite 1.0 to the large one (0.99).
- Softmax pushes the large value very close to 1.0 and others very close to 0.0, which is often desired for focusing attention.
- Numerical Stability: Implementations (like PyTorch’s) often subtract the maximum value before exponentiation () to prevent overflow errors with large numbers while mathematically yielding the same result.
In Classification Output
In a classification neural network, the Softmax function is applied to the output layer to interpret the neuron outputs as confidence scores or probabilities for each class.
- The output of each neuron represents the confidence that the input belongs to that specific category.
- All confidence scores sum to 1.
- Example: An output of
[0.7, 0.1, 0.2]implies a 70% confidence for the first class (e.g., Red).

